Introducing Quadratic Noise - A Better Perlin Noise

Perlin noise is among the most widely used algorithms in computer graphics and procedural generation. In particular, its a critical component of terrain generation, texturing 3D models, and many visual effects. For this reason, nearly every game engine and 3D modeling program provides an implementation of Perlin noise.

One of the biggest problems with Perlin noise is grid artifacts. These are visual patterns in the noise output aligned to the axis of the underlying coordinate space.

lines like these tend to occur on the vertical, horizontal, or diagonal axis in Perlin noise.

Many attempts have been made to fix this problem, including by Ken Perlin, the creator of Perlin noise, who designed Simplex noise:

While Simplex Noise does have less directional artifacts, it has some of its own problems:

• It is significantly slower then Perlin noise.

• It is difficult to make periodic.

• It is complex to implement, especially in 3+ dimensions.

For this reason, I developed a modified version of Perlin noise that I’m calling Quadratic noise. It’s a small modification to Perlin Noise that comes with a small performance cost (~20%) and reduces grid artifacts.

Here is some Quadratic Noise:

And here is some Perlin Noise for comparison.

Here is the Quadratic Noise contour line at zero:

And Perlin Noise for comparison:

So how does it work?

In Perlin noise, each integer coordinate pair in the 2D plane is assigned a random linear gradient. These gradients are then interpolated to produce the final result. In Quadratic noise, the output of these linear gradients are run through the quadratic function f(x) = x + x^2 * c before interpolation. C is a random coefficient generated for each gradient. Here what this looks like in pseudo-code:

float EvalGradient(int2 gradOrigin, float2 gradOriginToSamplePoint)
{
    float2 gradientVector = GetRandomGradientVector(gradOrigin);
    // evaluating the gradient
    float gradResult = dot(gradientVector, gradOriginToSamplePoint);
    // in perlin noise you just return gradientResult here.
    // in quadratic noise, you add a quadratic term before returning:
    gradResult += gradResult * gradResult * GetRandomNumber(gradOrigin);
    return gradResult;
}

The implementation of GetRandomGradientVector() and GetRandomNumber() can vary, however they should be deterministic and seeded by gradOrigin. In Perlin noise implementations, GetRandomGradientVector() typically returns a vector with magnitude close to 1, and I still recommend this for Quadratic noise. For GetRandomNumber(), I currently think randomly choosing between -1.5 and 1.5 looks the best, but this can be tuned to taste.

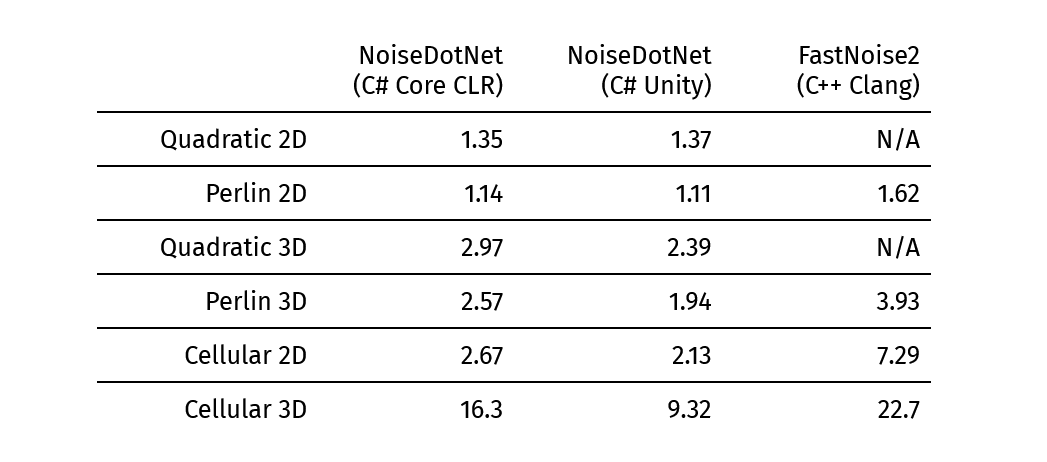
If you’d like to use Quadratic noise, I just published NoiseDotNet, an open-source C# library with extremely optimized implementations of Quadratic and Cellular noise in 2D and 3D. Here is a performance comparison with the excellent C++ library FastNoise2:

Unit is nanoseconds per sample. Profiled on a Ryzen 9 6900HS.

I’ll be following up this post with a deep dive into the optimization process for Perlin and Quadratic noise, so subscribe if that’s something you are interested in :)